前缀和

给定一个序列，长度为$n$，$m$次询问，求某一段区间的和。

一个一个加，复杂度$O(nm)$

有没有办法加速！

设数组是 $a[1]\sim a[n]$，我们求它的前缀和数组 $s[1]\sim s[n]$

其中，$s[i]=a[1]+a[2]+\dots a[i]=\sum _{k=1}^{i}a[k]$

这个数列很好递推求出来 $s[i]=s[i-1]+a[i]$

当我们求 $a[l]\sim a[r]$ 的和的时候，只需要 $s[r]-s[l-1]$

这样，预处理和单次查询复杂度是 $O(n)-O(1)$

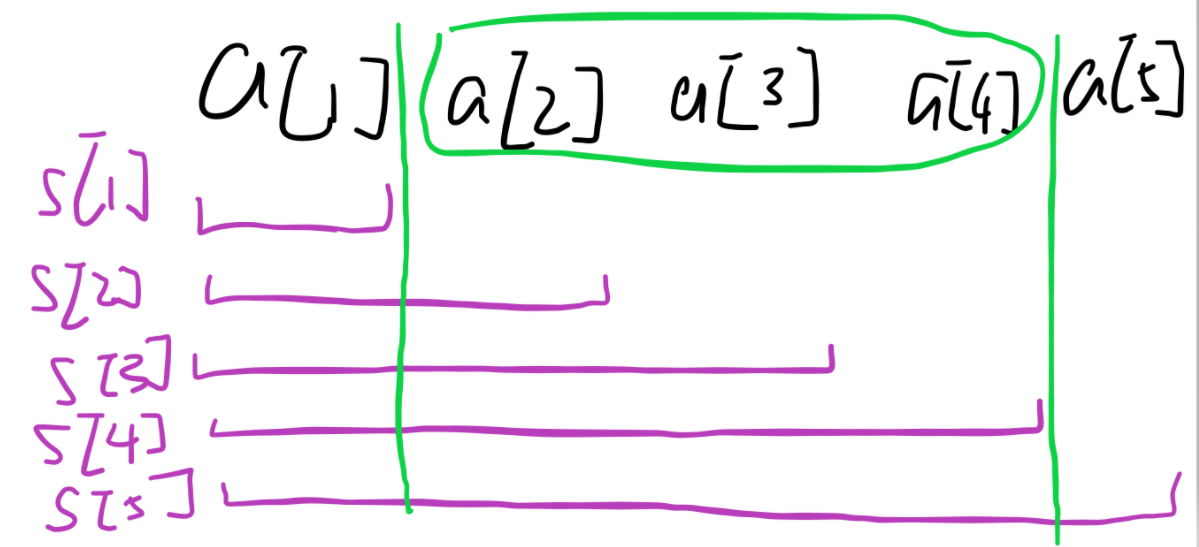
如图，$a[2]\sim a[4]$ 的和只要让 $s[4]-s[1]$ 就能得到。

该算法不支持在询问途中对原数列进行任何修改！

前缀和算法适用于操作存在逆操作的情况，比如加法的逆操作是减法，所以可以求区间的和。

或者比如乘法的逆操作是除法，所以也可以求区间乘积。

但是有的操作不可逆，比如取最小值，即使我们知道了 $a[1]\sim a[l-1]$ 的最小值和 $a[1]\sim a[r]$ 的最小值，也求不出 $a[l]\sim a[r]$ 的最小值，因为取最小值没有逆向操作。

差分

前缀和的逆操作

设有数组 $a[1]\sim a[n]$，求它的差分数组 $b[1]\sim b[n]$。

其中，$b[i]=a[i]-a[i-1]$

这样，$a[i]=b[1]+b[2]+\dots +b[i]$。

也就是说，差分是前缀和的逆操作

形式化地表示，我们设$\sum a$表示序列$a$的前缀和序列，$\mathrm{\Delta }a$表示序列$a$的差分序列，那么有：

$$\mathrm{\Delta }(\sum (a))=\sum (\mathrm{\Delta }(a))=a$$

我现在要将 $a[l]\sim a[r]$ 全部$+k$，一个一个加是 $O(n)$

如果用差分，我们可以在 $b[l]+k$，在 $b[r+1]-k$。

0 0 0 k 0 0 0 -k 0 0 0

然后再前缀和回去，可以发现，在 $l$ 以及之后的位置，因为都要加上 $b[l]$，所以这部分位置的值都加了 $k$。

在$r$之后的位置，因为都要加上 $b[r+1]$，所以又把之前加上的 $k$ 减掉了，相当于没变。

0 0 0 k k k k 0 0 0

这样我们就实现了$a[l]\sim a[r]$ 全部加 $k$。

如果是多次询问，那每次询问只要 $O(1)$ 的时间

预处理和单次查询的时间复杂度是 $O(n)-O(1)$

该算法不支持在修改途中对原数列进行任何查询，只能所有修改都完成后再查询。

高维前缀和

如果我的数组不是一维的，阁下又将如何应对？

比如是二维的，那么我们有二维原数组$a[i][j]$

那么对应的，有前缀和数组$s[i][j]=\sum _{t1=1}^i\sum _{t2=1}^{j}a[t1][t2]$

也可以通过递推得到：

s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

即 黑色= 紫色 + 绿色 - 蓝色 + 右下角（$a[i][j]$）。

如果我们要求左上角是$(x_1,y_1)$，右下角是$(x_2,y_2)$部分的面积

ans=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];

即 红色 = 紫色 - 蓝色 - 绿色 + 棕色。

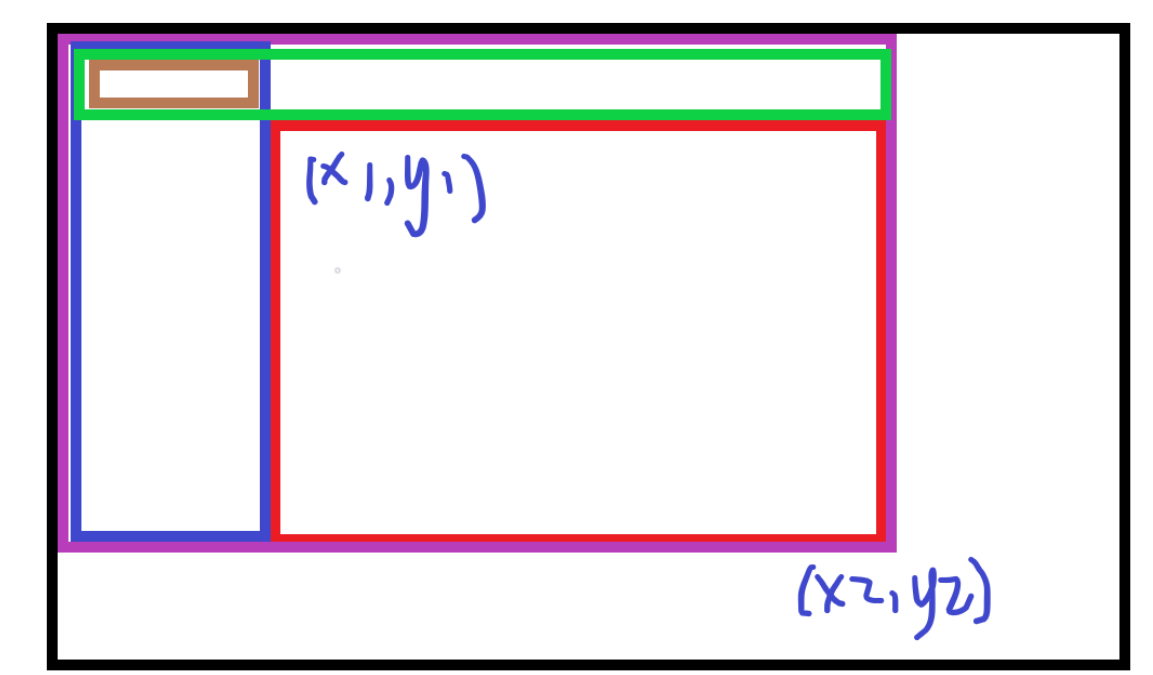
红色面积等于紫色减去蓝色减去绿色减去棕色。

这样对二维来说还可以，但是维度再增高之后就会出现弊端：

这个前缀和数组的算法，其实我们是在对多个维度进行容斥原理：

s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];

把只有一个维度降低的部分加上，把两个维度都降低的部分减去。

如果升到$k$维，那么我们预处理一个位置就要花$O(2^k)$的时间

采用另一种方法，一维一维的进行前缀和：

for(int j=1;j<=m;++j)
    for(int i=1;i<=n;++i) s[i][j]=s[i-1][j]+a[i][j];
for(int i=1;i<=n;++i)
    for(int j=1;j<=m;++j) s[i][j]=s[i][j-1]+s[i][j];

第一个求和是把第一维做前缀和，即 $s1[i][j]=\sum _{k=1}^{i}a[k][j]$

第二次求和再把第二维做前缀和，即 $s2[i][j]=\sum _{k=1}^{j}s1[i][k]$。

这样平均每个位置花费的时间就是$O(k)$。

高维前缀和常用的一个方向是统计一个二进制数字的子集和：

如果 $x|y=y$，则称 $x$ 是 $y$ 的二进制子集，数学表示为 $x\subset y$

设 $f(s)=\sum _{sub\subset s}a[s]$，则称 $f(s)$ 是 $s$ 的子集和。

比如 $5(101)$ 的子集有$5(101)$，$4(100)$，$1(001)$，$0(000)$。

对于一个二进制数，假设它有 $k$ 位，我们可以看作是一个 $k$ 维的前缀和，每一位是一个维度，利用上面讲的高维前缀和的方法求出子集和：

先枚举维度，然后把这一维度是 $1$ 的地方加上这一维度是 $0$ 的地方的值。

for(int i=0;i<k;++i)
{
	for(int s=0;s<(1<<k);++s)
	{
		if((s>>k)&1) f[s]+=f[s^(1<<k)];	
	}
}

高阶差分

差分可以让 $a[l]\sim a[r]$ 都 $+k$。

有没有让 $a[l]\sim a[r]$ 分别加 $1,2,3,\dots ,r-l+1$ 的方法。

有的，我们先求出 $a$ 数组的二阶差分数组 $c$。

即 $c=\mathrm{\Delta }(b=\mathrm{\Delta }(a))$，（$b$是$a$的差分，$c$是$b$的差分）

for(int i=n;i>=1;--i) b[i]=a[i]-a[i-1];
for(int i=n;i>=1;--i) c[i]=b[i]-b[i-1];

然后给 $c[l]+1,c[r+1]-1$。

0 0 0 1 0 0 0 0 -1 0 0 0

此时将$c$ 数组做前缀和得到 $b$ 数组，那么 $b[l]\sim b[r]$ 就会都加一。

0 0 0 1 1 1 1 1 0 0 0 0

此时给 b[r+1] 位置再减去一个 $r-l+1$

0 0 0 1 1 1 1 1 -5 0 0 0

再将 $b$ 数组做前缀和得到 $a$ 数组

那么 $a[l]$ 就会 $+1$，$a[l+1]$ 因为被加了两次，会$+2$，就会产生$a[l]\sim a[r]$实现$+1,+2,+3,\dots +r-l+1$的效果。

0 0 0 1 2 3 4 5 0 0 0 0

同理还可以用三次差分做到区间加 1 3 6 10 15 的效果。

其实一阶差分可以给区间加零次多项式（常数）

二阶差分可以给区间加一次多项式（$f(x)=k_1\ast x+k_0$）

三阶差分可以给区间加二次多项式 （$f(x)=k_2\ast x^2+k_1\ast x+k_0$）。

综上，$k-1$ 阶差分，只要有合适的系数，就可以做到给区间加上 $k-1$ 次的多项式。

练习题

P8218 【深进1.例1】求区间和

P2367 语文成绩

P3406 海底高铁

T271585 【模板】二维前缀和

P3397 地毯

P1115 最大子段和

P1719 最大加权矩形

P1314 [NOIP2011 提高组] 聪明的质监员