树状数组
前缀和
犹记前缀和数组:

支持
为什么修改这么慢呢,因为对于
导致查询和修改的耗时太不平衡了
为了平衡,我们给每个前缀和数组不要让他从记录从开头到当前位置的数值。
有一种方法是,每个位置记录
即每个位置记录当前位置到之前
每次查询,可以一下得到
int l,r;cin>>l>>r;
int sum=0;
while(r-l+1>=k)
{
sum+=s[r];
r-=k;
}
for(int i=l;i<=r;++i) sum+=a[i];2
3
4
5
6
7
8
这样查询的时间复杂度是
修改的时候,因为每个位置只被
int p,v;
cin>>p>>v;
for(int i=p;i>p-k;--i) s[i]=s[i]-a[p]+v;
a[p]=v;2
3
4
修改时间复杂度是
可以证明
既然事已至此,我们不妨把它更形式化一点,每
分块不是本节的重点,这个算法可以去分块那一章了解。
有一种更灵活的记录方式,可以将复杂度进一步降低
对于位置 lowbit(x)
假设
那么
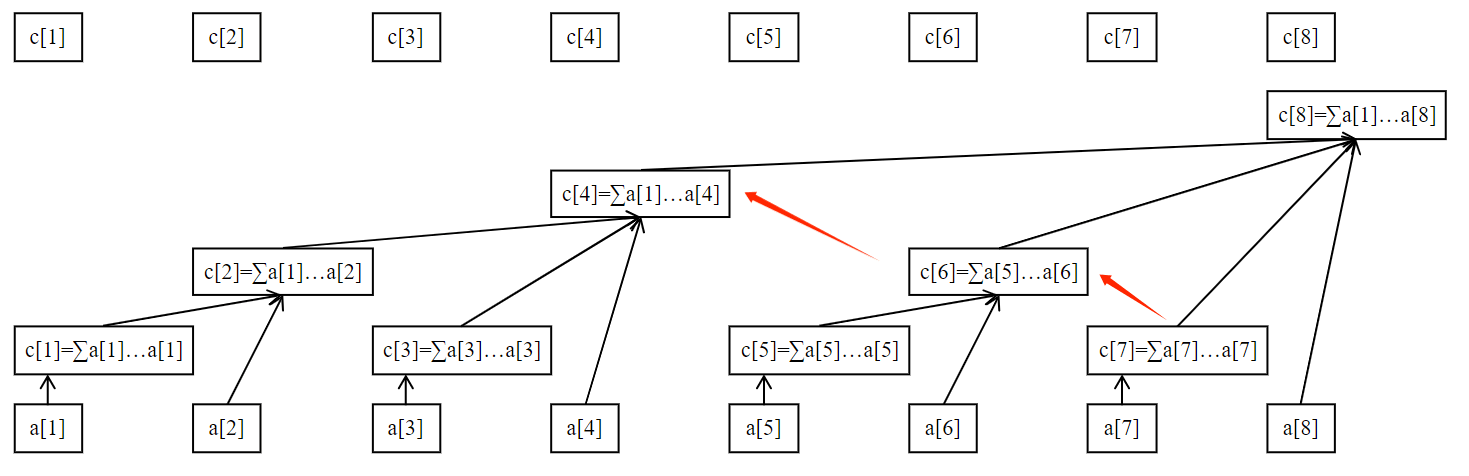
即从储存了
(图源:oiwiki)
求
例如求
由此得:至多
int r;cin>>r;
int sum=0;
while(r) sum+=s[r],r-=lowbit(r)2
3
当需要修改位置
每个位置的 lowbit 至少差了 lowbit 个位置)
涉及到的位置其实就是图中黑线指向的所有节点
int x,k;cin>>x>>k;
while(x<=n) s[x]+=k,x+=lowbit(x)2
和前缀和意义,如果是查询一个区间
所以它也维护的信息具有可减性,或者说具有逆元。
lowbit
在这里补充说明以下如何快速求
计算机中存储负数时用的是补码(这个概念这里不介绍)
因为补码是原本的二进制取反再
原本
例如:
那么
再给反码
此时除了最低为,其他位均与
所以 lowbit(x)=x&-x。
例题:
P3374 【模板】树状数组 1 动态前缀和
P3368 【模板】树状数组 2 动态差分
树状数组支持单点修改和区间查询,在这两个功能的基础上可以实现动态前缀和(区间查询)和动态差分(单点修改)
前缀和:查询
差分:查询
树状数组可以说是平衡了两者的时间复杂度。
值域
给定一个
根据定义,是要求每个数字前面有多少大于自己的数字
对
然后每次统计完,再给
for(int i=1;i<=n;++i)
{
ans+=query(n)-query(a[i]);
update(a[i],1);
}2
3
4
5
练习题
P1972 [SDOI2009] HH的项链 特别重要的题,一定要会

