并查集

$n$个点，有$m$次操作，每次操作如下：

$1.$把 $x,y$ 连接起来。

$2.$ 问$x,y$ 是不是被直接或间接连接起来了。

怎么把 $x,y$ 连起来呢？

哈哈，直接连双向边就行了。查询的时候从一个点开始$dfs$找另一个点。

但是这样，连接-查询是$O(1)-O(n)$的，查询复杂度太高了。

我们给每个点设置一个老大，一开始所有人的老大都是自己。（牢大，想你了）

for(int i=1;i<=n;++i) f[i]=i;//f[i]表示i的老大是谁。

如果两个点要连边，那么就把其中一个人的老大设置成另一个人。

比如$1,2$连边，$1,3$连边：

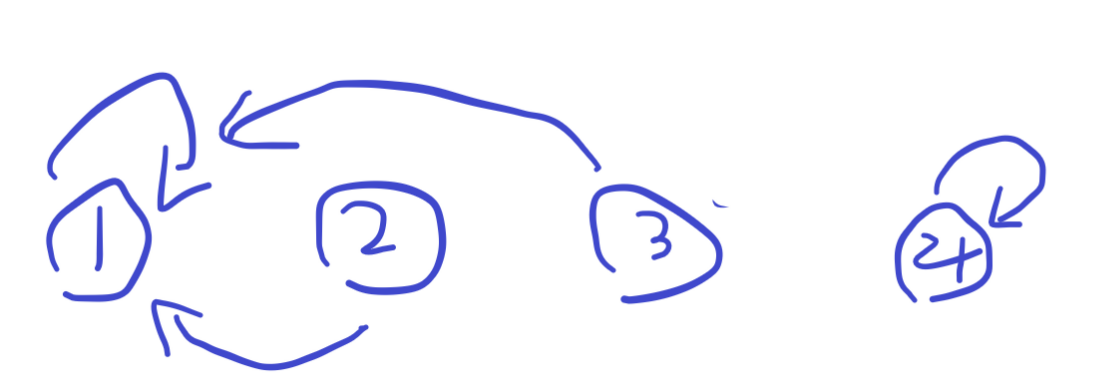
如果两个人的老大是同一个人，那么说明这两个人是一伙的。

这个老大要找的是最终的老大，因为有可能长这样：

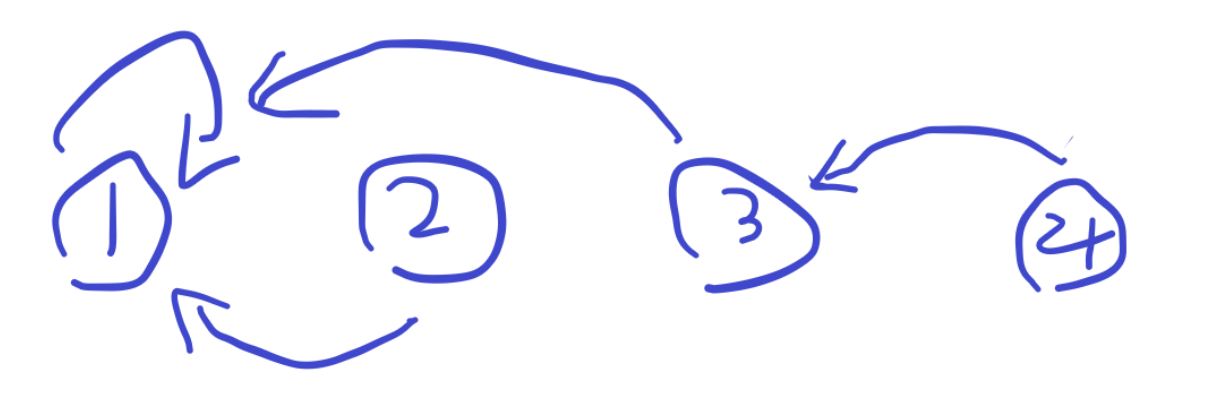
这时候$2,4$也是一伙的，所以找老大要找到最终的老大为止。

int find(int k)
{
	if(f[k]==k) return k;//如果老大是自己，返回自己。
	return find(f[k]);否则继续找老大的老大
}

但是这样有问题，比如先连了$1,2$和$3,4$，这时候再连$2,3$，就会出现这种情况：

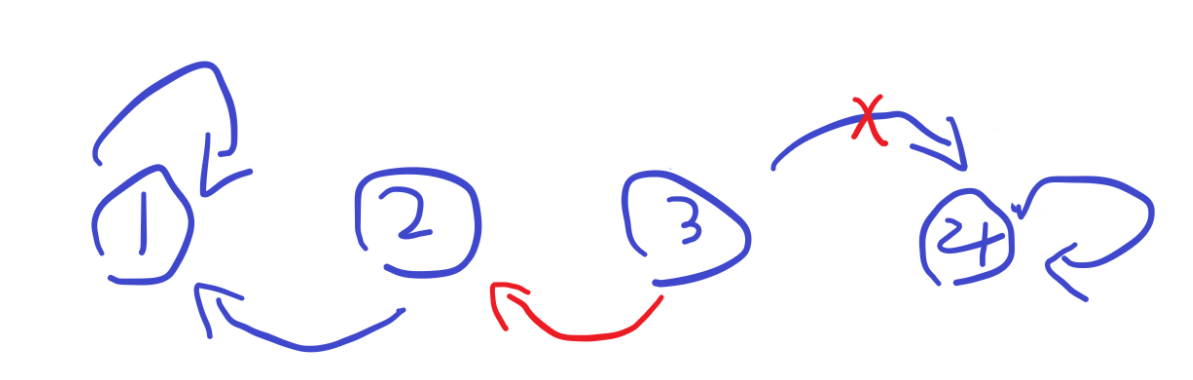
本来$4$已经收了$3$做小弟，这时候$3$偷偷跟着$2$跑了，这样就不对了（因为此时按理来说，$1,4$应该联通）。

这时候可以这样理解，$2,3$干了一架，$3$打输了，但是$3$不能直接投降，应该找自己的老大$4$给自己出气。

以此类推，其实这场架是双方的最终老大在干架，所以应该把双方的最终老大连起来。

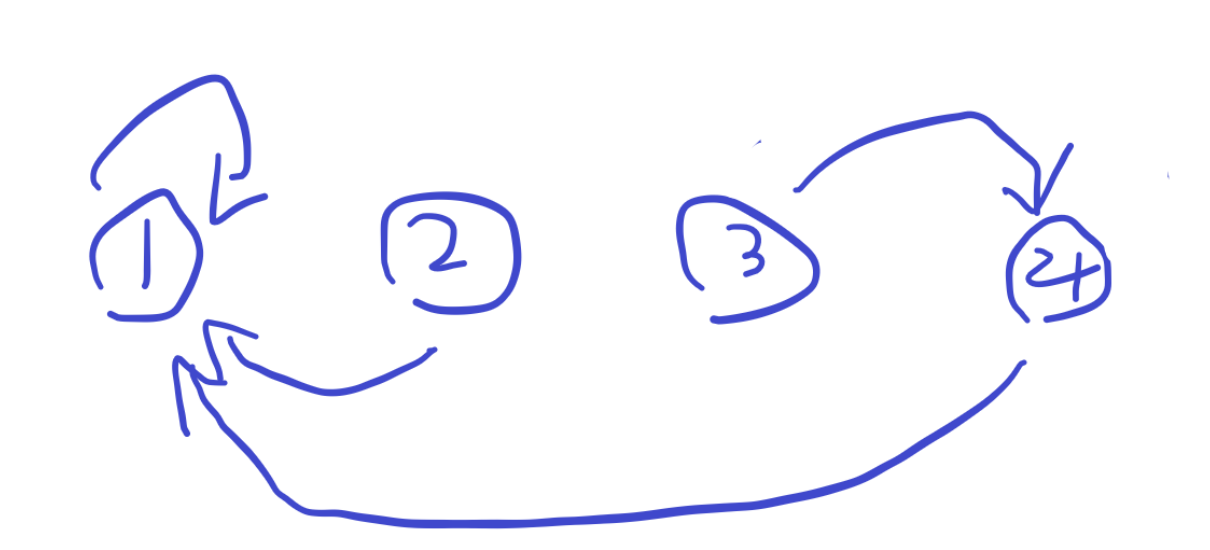
void merge(int x,int y)//连接x,y
{
    if(find(x)==find(y)) return;//如果两个人其实是一伙的，跳过。
    f[find(x)]=find(y);//两个人的最终老大合并了。
}

但是这样查询的复杂度还是$O(n)$，万一整个关系形成一条好长好长的链怎么办？

我们有办法！这个图的形态要比一般的图简单很多，所以可以考虑一些优化方法。

路径压缩

首先，我们判断某两个点是不是联通，只需要一个信息，就是点的最终老大是谁。

所以我们连这么长一条链是没有用的，不如在查询的时候做一点手脚：

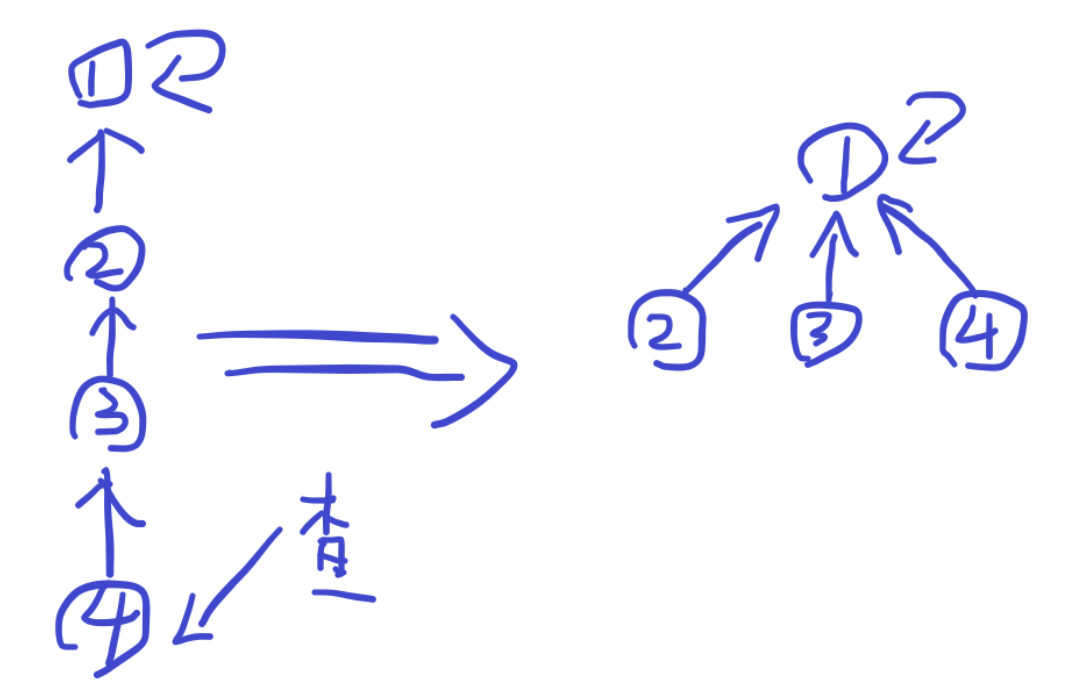
我们将查询路径上遇到的点，全都直接去接到最终的老大下面。这样下次再查的时候直接$O(1)$出结果了，非常方便。

int find(int k)
{
	if(f[k]==k) return k;
	int t=find(f[k]);
	return f[k]=t;
}
/*
更简单的写法
int find(int k){return f[k]==k?k:f[k]=find(f[k]);}
*/

复杂度分析：我也不太会

单纯的加上的路径压缩，单次查询复杂度上界是$O(logn)$

按秩合并

（其实是一种启发式合并）

还有另一个办法：如果我们不想破坏这个链的形态，也就是我们还关心每个点的直接老大是谁，那么可以用按秩序合并。

在合并两个最终老大的时候，之前没有去管哪个接在哪个下面，这里其实可以优化。

设两个最终老大$x,y$，$x$下面连了$k_1$层节点（最大深度为$k_1$），$y$下面连了$k_2$层节点（最大深度为$k_2$）。

不妨假设$k_1\le k_2$。

如果$k_1<k_2$，那么接上去之后因为原本的根$x$变成了一层子节点，所以所有节点的深度都$+1$了。但是$k_1+1\le k_2$，所以最大深度没有变。

如果$k_1=k_2$，那么接上去，$x$子节点的最大深度变成了$k_1+1$，

所以我们每次把深度比较小的那个接到大的下面。

如果两个节点的最大深度不同，那么花费的最大时间是没变的（单次查询花费的最大时间就是深度，因为每次走一步。）

所以当且仅当两个节点的最大深度相同的时候，平均花费时间才会$+1$。

然而这个$+1$的次数是很少的。

假设单个节点的深度是$1$，要形成一个深度为$2$的集合，至少需要$2$个节点，要形成一个深度为$3$的节点，至少需要两个深度为$2$的节点，也就是$4$个节点，以此类推，$n$个节点按这个规则合并，最大深度是$O(logn)$的。

int f[N],r[N];//r表示深度
void merge(int x,int y)
{
	x=find(x),y=find(y);
	if(x==y) return;
	if(r[x]>r[y]) swap(x,y);
	f[x]=y;
	r[y]+=(r[x]==r[y]);
}

注意这里的想法类似启发式合并，但这里是按深度由小向大合并，因为在并查集中，复杂度是和深度有关的，而不是节点个数。

如果两个优化方法一起用，单次复杂度是 $O(\alpha )$ （反阿克曼函数），约等于线性 $O(1)$。

删除

若要删除，则将自己的牢大重新指向自己。

这要求的原本的机构不被破坏，即只能用按秩合并，不能用路径压缩。

P1551 亲戚

扩展域并查集

给每个点一个反义节点，用来维护不同种类的关系问题。

通常用法是判断一个图是不是二分图（即图中所有节点的可以分为两部分，同一部分的节点之间互相没有边，或者说每一条边的两边节点都属于不同的部分，最多有两个部分）也可以用并查集：

假设有$n$个点，我们把这$n$个点每个点都复制一份，编号为$n+1\sim n+n$。

如果两个点 $x,y$ 之间有一条边，那么我们把 $(x,y+n)$ 和 $(x+n,y)$ 用并查集连起来。

这样就代表着，$x,y$ 在不同的部分里。

假如之后连边是这样的：

$x,z$ 连边，$y,z$ 连边。

那么 $(x+n,z)$ 在一个集合，同时 $(x+n,y)$ 在一个集合

在试图把 $y,z$ 连边的时候，发现 $(y,z)$ 已经在一个集合里了，这说明 $(y,z)$ 属于二分图中的同一个部分，再连边就破坏了二分图的性质了。

P1525 [NOIP2010 提高组] 关押罪犯

带权并查集

并查集向上的边也可以携带一些信息：

食物链

有三类生物，$A,B,C$，$A$吃$B$，$B$吃$C$，$C$吃$A$。

有两种关系：$x,y$是同一类生物，或者$x$吃$y$。

给定关系，如果新给出的关系和已经有了的关系冲突，就是假话，问有多少句假话。

我们把三种关系分别标号为$0,1,2$。设$x$的种类为$b(x)$

如果$(b(x)+1)\mathrm{\%}3==b(y)$，那么$x$就会吃$y$。

那么可以在并查集连边的同时，维护一个信息$(0/1/2)$，如果$x->y$这条边的权值是$1$，那么表示$x$吃$y$，如果这条边权值是$2$，那么表示$y$吃$x$，如果权值是$0$，表示$x$和$y$是同类。

那么比如$x->y->z$这两条边的权值都是$1$，那么$x$吃$y$，$y$吃$z$，$z$吃$x$。

$z$吃$x$怎么表示出来呢，会发现$x$到$z$的路径和刚好是$2$，所以表示$z$吃$x$。

也就是两点之间的路径和对$3$的模数代表了这两个点之间种类的关系。

练习题

P1621 集合

P1197 [JSOI2008] 星球大战

P1196 [NOI2002] 银河英雄传说

P1955 [NOI2015] 程序自动分析

P1682 过家家