记忆化搜索与动态规划

记忆化搜索

前面已经提到了，我们在搜索的时候，有时候多个状态会指向同一个状态。

比如，把整数 $n$ 分解成 $k$ 个数字有多少种方案数。

那么前两个数字不管是 $1, 3$ 还是 $2, 2$ ，都会到达把 $n - 4$ 分解成 $k - 2$ 个数字这个状态。

所以我们可以进行记忆化，就是在第一个到达 $(n - 4, k - 2)$ 这个状态的时候，把算出的方案数记录下来，第二次再来的时候直接返回数组里存的数。

cpp

int dfs(int n,int k)
{
    if(k==0)
    {
        return (n==0);
    }
    if(dp[n][k]!=-1) return dp[n][k];
    int ret=0;
    for(int i=1;i<=n;++i)
    {
        ret+=dfs(n-i,k-1);
    }
    dp[n][k]=ret;
    return ret;
}

这里，dfs 的参数有两个，取值范围分别是 1~n 和 1~k 。

dfs 内部还有一个循环，所以总时间复杂度 $O (n^{2} k)$ 。

这样也可以改成递推的形式：

cpp

dp[0][0]=1;
for(int i=1;i<=k;++i)
{
    for(int j=0;j<=n;++j)
    {
        for(int x=1;x+j<=n;++x)
        {
            dp[x+j][i]+=dp[j][i-1];
        }
    }
}

但是在有些情况下，递归比递推更容易表示出来。

P1434 [SHOI2002] 滑雪

P2196 [NOIP1996 提高组] 挖地雷

P4017 最大食物链计数

动态规划（DP）

动态规划可以解决一些只顾眼前利益的贪心解决不了的问题。

比如，有 $n$ 颗宝石，每颗价值是 $v_{i}$ ，价格是 $w_{i}$ ，要求在总价格不超过 $W$ 的情况下让价值最大。

对于三颗宝石，（价格，价值）分别为： $(6, 9), (3, 4), (5, 6)$ ，与此同时， $W = 8$ 的情况。

不管是先取价值最大的，还是先取性价比最高的，都选不到最优解（选后两个）

更不用说宝石更多时，情况更复杂。

怎么办呢，不能在当前选择时决定的情况，我们就把它加入到状态里去。

比如说，对于第一颗糖，它的价格是 $6$ ，价值是 $9$ ，那么它应不应该要我现在不知道，我把它要和不要的情况都记录下来。

如果要他，那么现在花了 $6$ 块钱，拿到了 $9$ 点价值，记录 $d p [6] = 9$ 。

如果不要，那么现在花了 $0$ 块钱，拿到了 $0$ 点价值，记录 $d p [0] = 0$ 。

然后对于下一个物品，假设价格是 $3$ ，价值是 $5$ ，那么

前面我们有花了 $0, 6$ 元的情况，再这个基础上拓展：

花 $0$ 元的基础上： $d p [3] = 5, d p [0] = 0$

花 $6$ 元的基础上： $d p [9] = 14, d p [6] = 9$

这个不就是枚举每个物品要还是不要吗，那这样复杂度不就变成 $O (2^{n})$ 了吗。

假设下一个物品，价格是 $3$ ，价值是 $7$ 。

那么我们现在有四种情况： $0, 3, 6, 9$

假如我现在在 $3$ 元的基础上拓展，选择要这个物品，那么应该拓展到 $d p [6]$ 。

但是 $d p [6]$ 里面本来就有值了，这时候应该让 $d p [6] = m a x (d p [6], d p [3] + 7)$ 。

也就是将情况合并，只保留最好的结果。

所以这时候，一共只会保留下花了 $0 \sim W$ 元钱的状态各一个，一共 $n$ 个物品，所以复杂度是 $O (n W)$

例题一

数字三角形

设 $d p [i] [j]$ 为从 $(1, 1)$ 走到第 $i$ 行，第 $j$ 个位置时，已经获得的最大的和。

每个位置可以从上一行的这一个，或者上一行的左边一个转移过来。

$d p [i] [j]$ 可以表示为 dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j]

最后答案是 max{dp[r][i]}

DP三要素

1.最优子结构性质

即目前局面的最优解的通过某个抉择，从之前局面的最优解得到的：

比如上面的数字三角形问题：

dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j]

dp[i][j] 的最优解是从 dp[i-1][j-1] 和 dp[i-1][j] 其中之一的最优解，再通过一步抉择得到的。

如果 dp[i][j] 的最优解不能通过之前的最优解得到，那么问题就复杂了。

2.无后效性

确定转移顺序后，当前问题的最优解只和之前已经确定的局面有关。

比如上面的数字三角形问题：

当你按行去转移，枚举到 dp[i][j] 的时候，dp[i-1][j] 和 dp[i-1][j-1] 的值已经确定不会变了。

dp[i][j] 的值只和已经确定的 dp[i-1][j] 和 dp[i-1][j-1] 有关系。

如果 dp[i][j] 的值同时和 dp[i+1][j],dp[i-1][j] 有关系，那么不管怎么转移，dp[i][j] 都有后效性，就没办法动态规划了。

无后效性也可以理解为，如果把状态抽象成节点，把转移抽象成节点之间的一条有向边，那么这张图是有向无环图（DAG）。

可以想象，如果这张图上有环，那么环上节点的信息通过转移永远也不能确定下来。

有向无环图和动态规划问题因此可以互相转化。

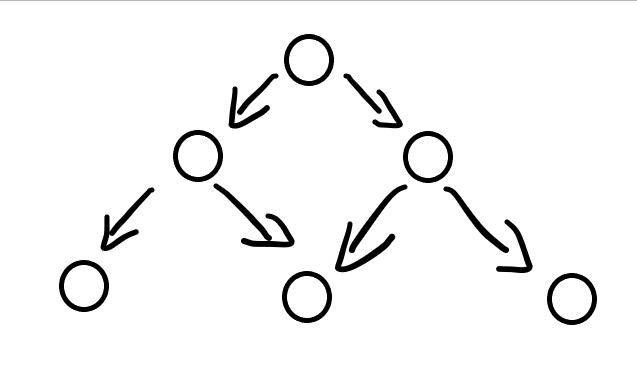
3.缩小问题规模

当你做出一步觉得后，接下来要解决的问题和之前要解决的问题类似，只是问题规模变小了。

比如 $n$ 个数里面选 $k$ 个方案数，当第一个数字选择 $2$ ，接下来的问题是 $n - 2$ 个数字选择 $k - 1$ 个，和原问题几乎一致。问题规模减小。

例题二：

有 $n$ 个位置，第 $i$ 个位置上有数字 $a_{i}$ ，选择任意多个位置让选择的位置上的数字和最大，但是不能选相邻的两个位置。

怎么做呢，对于第 $i$ 个位置，它选不选还要取决于第 $i + 1$ 个位置选还是不选，这时候贪心就很难抉择，我们称这个信息有后效性。（如果所有位置上的数字都是 $1$ ，那就能选则选，因为这是前面讲过的不会更优类贪心）

DP常用方案：对于有后效性的部分，把它加进状态里！

设 dp[i][0/1]表示，已经处理了 $1 \sim i$ 所有的位置，其中第 i 个位置选还是不选。

dp[i][0] 表示第 $i$ 个位置不选的最大值，dp[i][1] 表示第 i 个位置选的最大值。

既然有后效性，那就把方案都记录下来。

当我们处理下一个位置时：

dp[i+1][0]=max(dp[i][1],dp[i][0])：如果下一个位置不选，这个位置选不选都行。

dp[i+1][1]=dp[i][0]+a[i+1]：如果下一个位置选，这个位置只能不选了。

答案就是 max(dp[n][0],dp[n][1])

练习题

P1002 [NOIP2002 普及组] 过河卒

P1095 [NOIP2007 普及组] 守望者的逃离

P1077 [NOIP2012 普及组] 摆花

P3842 [TJOI2007] 线段

P1020 [NOIP1999 普及组] 导弹拦截用到了二分优化和最小链覆盖等与最长反链

P4059 [Code+#1] 找爸爸