背包 | 动态规划

01背包

背包问题： $n$ 个物品，每个物品价值是 $v_{i}$ ，重量是 $w_{i}$ ，一个最多承重为 $W$ 的背包，每个物品最多选择一次，能装的价值和最多是多少。

上一节已经介绍过这个问题不能贪心了。

设 dp[i][j] 表示，前 i 个物品，已经装了的物品总重量是 j 时的最大值。

枚举到第 i 个物品时，就两种选择，这个物品选或者不选。

不选：dp[i][j]=max(dp[i][j],dp[i-1][j])

选：dp[i][j]=max(dp[i][j],dp[i-1][j-w_i]+v_i)

时间复杂度 $O (n m)$ ，空间复杂度 $O (n m)$

总结成代码

cpp

int n;cin>>n;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i)
{
for(int j=0;j<=m;++j)
{
dp[i][j]=dp[i-1][j];//不选这个物品
if(j>=w[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);//选这个物品
}
}

滚动数组

我们发现，其实有优化的空间。

我们发现，当前状态 dp[i][j]，只和 dp[i-1][xxx] 有关系，和 dp[i-2][xxx] 以及再之前的都没关系了。

所以理论上我们只要保留两个第一维的信息，其他的可以丢掉。

我们只保留 dp[2][m]，然后当 i 是奇数的时候，从 dp[0][x] 向 dp[1][x] 转移，当 i 是偶数的时候，从 dp[1][x] 向 dp[0][x] 转移。

cpp

int n;cin>>n;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i)
{
int opt=i&1;
for(int j=0;j<=m;++j) dp[opt][j]=0;//因为之前可能用过这里，清空一下
for(int j=0;j<=m;++j)
{
dp[opt][j]=dp[opt^1][j];
if(j>=w[i]) dp[opt][j]=max(dp[opt][j],dp[opt^1][j-w[i]]+v[i]);
}

}

滚动数组pro max

我们发现不了，上面的滚动数组还有优化空间~

我们在进行转移时，dp[i][j] 是通过 dp[i-1][j] 和 dp[i-1][j-w[i]] 转移来的。

也就是说，dp[i][j] 只会从 dp[i-1][<=j] 的位置转移过来。

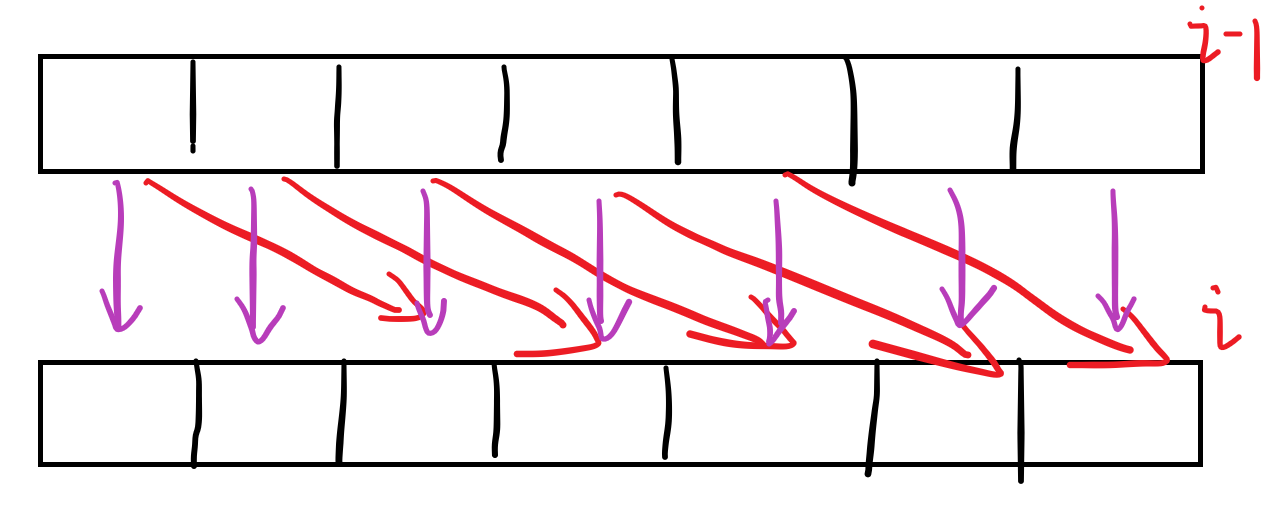
如果我们将两个数组合并成一个：

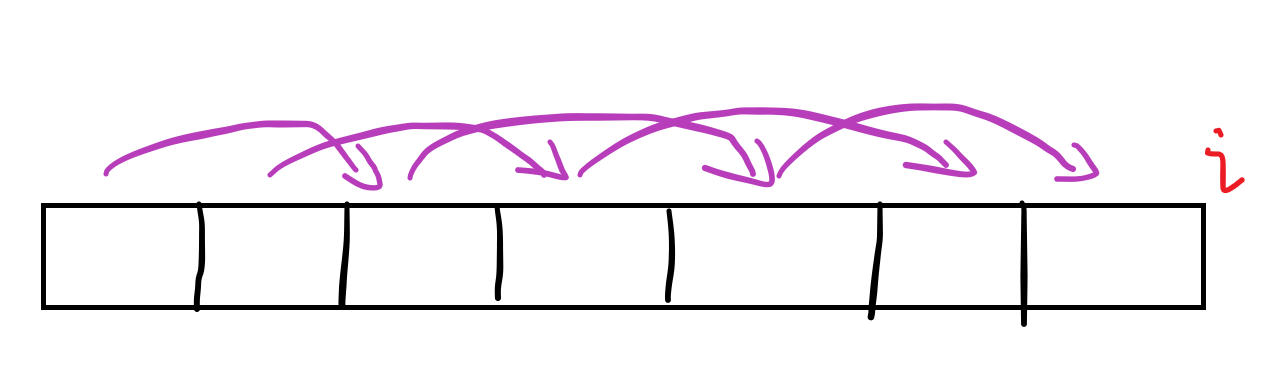
假如我们是倒叙更新 dp[i][m]~dp[i][0] 的，现在刚更新完第四个：

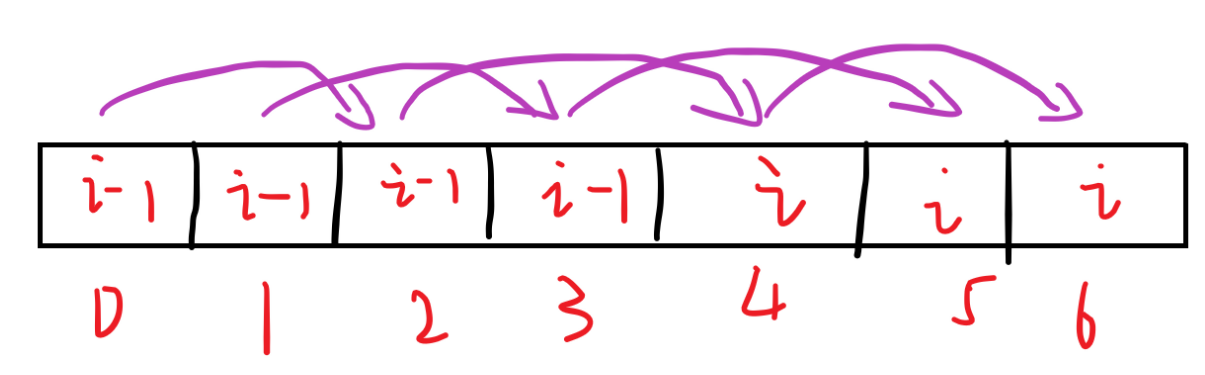
下一步更新 dp[i][3]=max(dp[i-1][3],dp[i-1][3-w[i]]+v[i]) （此处设 w[i]=2 ）。

发现 3 位置和 1 位置还没有更新成第 i 行的答案，刚好可以利用。

那么不如直接把两行信息合并。

每次更新按容量从大到小更新。

所以可以这样写

cpp

int n;cin>>n;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i)
{
int opt=i&1;
for(int j=0;j<=m;++j) dp[j]=0;//因为之前可能用过这里，清空一下
for(int j=m;j>=w[i];--j)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
//max()中，第一个其实是dp[i-1][j],第二个其实是dp[i-1][j-w[i]]+v[i]
}
}

如果正着更新，在第 $i$ 个物品时 dp[i][x] 会从 dp[i][x-w[i]]+v[i] 更新过来，而 dp[i][x+w[i]] 会被 dp[i][x]+v[i] 再更新一次，等价于这个物品被选择了两次，不符合题目要求。

无限背包

和 $01$ 背包相比，区别就是每个物品可以选择无限次。

刚好上面介绍了为什么不能正着更新，这个直接拿来正着更新就行。

cpp

int n;cin>>n;
for(int i=1;i<=n;++i) cin>>v[i]>>w[i];
for(int i=1;i<=n;++i)
{
int opt=i&1;
for(int j=0;j<=m;++j) dp[j]=0;//因为之前可能用过这里，清空一下
for(int j=w[i];j<=m;++j)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
//max()中，第一个其实是dp[i-1][j],第二个其实是dp[i-1][j-w[i]]+v[i]
}
}