贪心

两瓶一样的可乐，一瓶两块，一瓶三块，你买哪瓶。

选两块的？你已经学会贪心了！来做两个例题吧：

（一）

$n$个物品，价值各不相同，选$m$个物品的最大价值之和是多少？

解答：选最大的$m$个。

（二）

删数游戏：给一个 n 位的数字，从中删去 k 位，能得到的最小的数字是多少？

解答：

假设数字从高位到低位分别是 w[1],w[2],……,w[n] ，其中 0<= w[i]<= 9，w[1] 是最高位。

数字高位比低位的权重大，所以删数要优先让高位变得更小。

从高到低考虑应该删哪个数字：

for(int i=1;i<=n;++i)

如果 w[i]<=w[i+1] ：

如果删掉第 i 位或者之前的位，那么w[i+1] 做之后的第 i 位

如果删掉第 i+1 位或者之后的位，那么 w[i] 做之后的第 i 位。

为了尽可能小，应该删 i+1 及之后的位，跳过 i。

如果 w[i]>w[i+1]：

同理，为了尽可能小，应该删除当前的第 i 位。

综上，每次删除应该找到最靠左的满足 w[i]>w[i-1] 的位置，然后删除 w[i]。

如果不存在这样的位置，那就说明越靠右的数字越大，直接删去最后一位就可以了。

交换邻项

（一）

排队接水：$n$ 个人接水，第 $i$ 个人需要 $t_i$ 分钟，怎么安排队伍，让所有人等待的时长之和最小？

解答：

假设相邻的两个人 $a+1=b$，接水时间是 $t_a$ 和 $t_b$，并且 $t_a>t_b$。

这两个人前面有 $x$ 个人，后面有 $y$ 个人。

那么这两个人以及后面的人需要等的总时间是 $t_a\ast (y+2)+t_b\ast (y+1)$

假如这两个人交换一下位置，总时间变成了 $t_a\ast (y+1)+t_b\ast (y+2)$

明显变小了，所以应该交换一下。

很像冒泡排序的过程，当遇到相邻的左边大于右边时就交换。

所以可以直接按时间从小到大排序。

（二）

国王游戏：

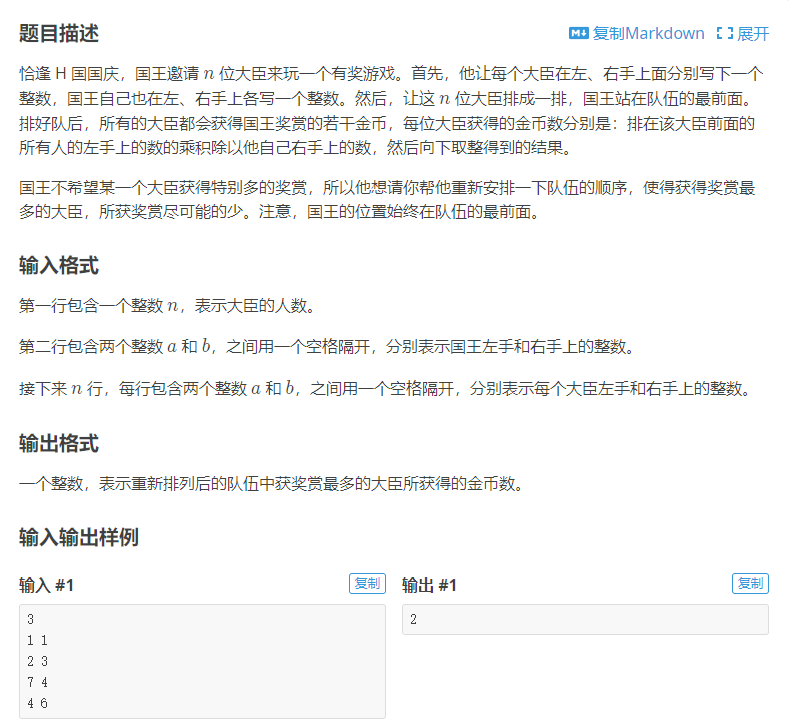
解答：

假设位置 $i$ 左手的数字是 $a_i$，右手是 $b_i$。

有相邻的两个位置 $i,i+1$，假如前面所有人左手上的乘积是$x$，那么原本的的贡献是：

$$max\{\frac{x}{b_i},\frac{x\ast a_i}{b_{i+1}}\}$$

如果 $i$ 和 $i+1$ 交换位置，贡献变成了：

$$max\{\frac{x}{b_{i+1}},\frac{x\ast a_{i+1}}{b_i}\}$$

如果是 $i$ 在前面比较好，那么应该满足

$$max\{\frac{x}{b_i},\frac{x\ast a_i}{b_{i+1}}\}<max\{\frac{x}{b_{i+1}},\frac{x\ast a_{i+1}}{b_i}\}$$

因为 $\frac{x}{b_{i+1}}$ 一定要小于 $\frac{x\ast a_i}{b_{i+1}}$，所以后面的最大值只可能是 $\frac{x\ast a_{i+1}}{b_i}$，它一定大于 $\frac{x}{b_i}$，那么只要让它大于 $\frac{x\ast a_i}{b_{i+1}}$

就是

$$\begin{gathered} \frac{x\ast a_i}{b_{i+1}}<\frac{x\ast a_{i+1}}{b_i} \\ {a}_i{b}_i<a_{i+1}{b}_{i+1} \end{gathered}$$

综上，把大臣们按$a_i\ast b_i$从小到大排序就好。

不会更差

（一）

线段选取：$n$ 个线段，最多能选出几个互不相交的线段？

解答：

考虑以某个顺序选取线段：

我们按从左到右的顺序选，反正不管选哪个线段也是答案 +1，所以希望当前选择的线段对之后的负面影响最小。

那么只要每次都选取能选择的线段中，右端点最靠左的线段，这样对右边的占用最少。

比如有两个线段 $[l1,r1]$ 和 $[l2,r2]$，因为是从左往右选，所以左端点在哪里无所谓，只要不和左边已经选了的线段冲突就行，而右端点要尽可能靠左，不然会更多地影响右边的选择，所以选右端点最靠左的线段，不会让之后的答案更差。

实现上：线段按右端点从小到大排个序，能选就选即可。

//按右端点从小到大排序
int pre=0,sum=0;
for(int i=1;i<=n;++i)
{
    if(a[i].l<pre)
    {
        pre=a[i].r;
        ++sum;
    }
}
cout<<sum<<'\n';

（二）

砍树：

在一个数轴的$n$个不同位置上有$n$棵树，每棵树都可以砍倒，砍倒后它会往左或往右倒下（不碰到其他树），最多砍几棵树？

解答：

我们还是从左往右考虑：

如果一棵树可以往左倒，那么一定会往左倒，因为对右边没影响。

如果可以往右倒，也一定会倒，为什么：

我们只考虑一种情况，就是因为这棵树往右倒了而导致下一颗树不能向左倒下的情况：

前一棵树倒下，后一棵树有可能会倒，只不过可能性降低了，贡献>=1

前一棵树不倒，后一棵树还是有可能会倒，贡献<=1

所以，前者直接向右倒，至少不会让答案变得更差，还有可能变得更好，就可以直接选择倒。

贪心中常用的工具

$STL$数据结构——堆

一种数据结构，粗略来看，可以视作一个集合，每次可以把里面最大的/最小的数字拿出来。

$C++$里面有很方便的工具：

priority_queue<int> q;//定义一个堆，名字叫q
for(int i=1;i<=n;++i)
{
    int x;cin>>x;
    q.push(x);//把n个数字放进堆里
}
int y=q.top();//取出堆里面最大的数
q.pop();//把最大的数删掉。

priority_queue 表示声明一个堆，<int> 是确实这个堆里存的是什么类型的变量 ， q 是定义出来的堆的名字。

堆定义起来默认是大根堆，就是堆的最上面的最大的数字。

如果想取最小的数呢？

priori_queue<int,vector<int>,greater<int> > q;//小根堆

这样，上面的操作中取出的就是最小的数。

堆里面既然可以存最大、最小，那么说明存的数据类型必须是可以排序的，才有最大最小一说。

如果堆里想存结构体的话：

struct node
{
	//一些类型
    int x;//用来排序的数值
    bool operator < (node t)
    {
        return x<t.x;
    }
};

这个函数是重新定义 node 类型的结构体中小于号的含义。

其中 operator 是重载的意思，后面跟着 < 表示这个函数要重新定义小于号的含义，其中小于号的返回值是 bool 类型。

函数的参数是另一个结构体，也就是你用来对比的那个结构体。

这里不用写两个比较参数，因为默认第一个参数是你这个结构体本身，所以里面的第一个x 不用指明来自哪个结构体。

然后在里面指定你的比较规则，之后它就可以放进堆里了。

练习题

P2240 【深基12.例1】部分背包问题

P1106 删数问题

P1223 排队接水 .

P1080 [NOIP2012 提高组] 国王游戏

P1803 凌乱的yyy / 线段覆盖

Woodcutters

P1090 [NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G