BFS

深度优先搜索会向着一个方向一直走，走到头为止，再退回去尝试其他路线，而广度优先搜索是在每个方向上都一步一步地走。

$D F S$ :（数字标号是访问节点的顺序）

$B F S$ :

$D F S$ 的好处是方便通过已经得到的答案进行一些优化和剪枝，而 $B F S$ 方便测量某个节点距离初始节点的距离。

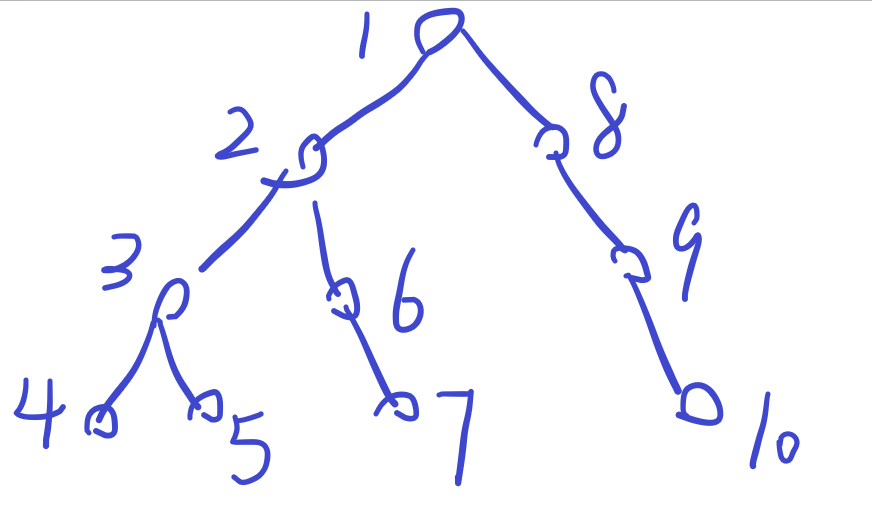
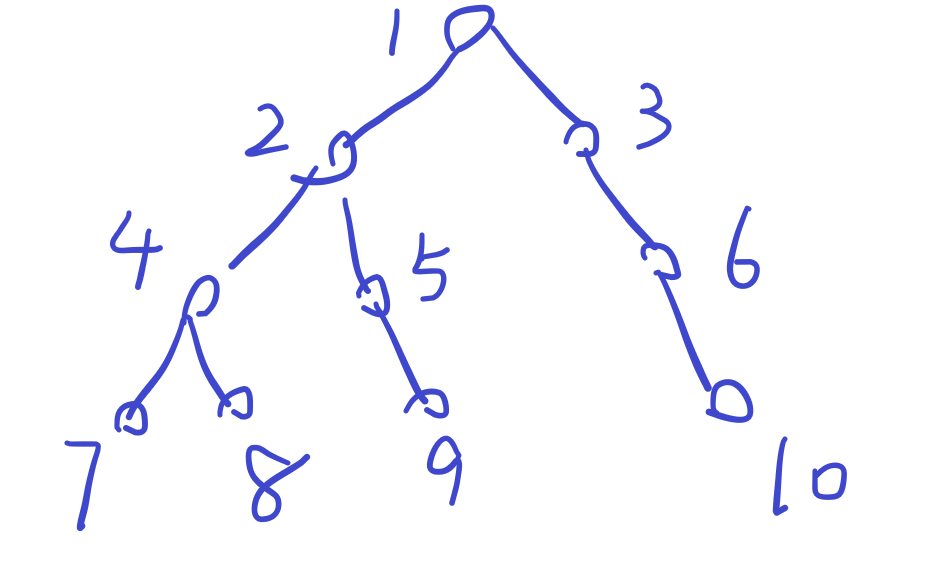
例如：

有一个 $n \times m$ 的棋盘，在某个点 $(x, y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

从初始点 $V_{0} = (x, y)$ ，先看看走一步能到哪些点集 $V_{1}$ 。

再从$ V_1$ 出发，到达下一组位置 $V_{2}$ ，如果下一步到达的点已经在 $V_{0}$ 或 $V_{1}$ 中出现过了，则跳过这个点。

依次类推，直到所有能到达点都走过。

模拟这个过程，用队列比较合适

一开始只有初始节点在队列里：

找到 $V_{0}$ 能到的位置，把他们记作 $V_{1}$ ，放入队列：

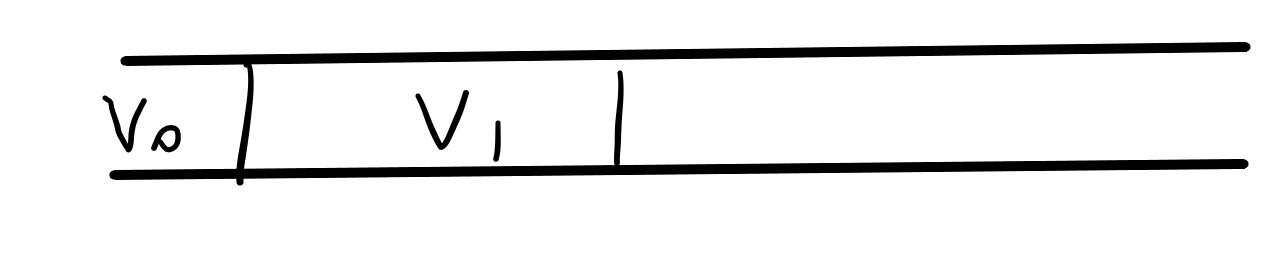
然后此时 $V_{0}$ 就已经把能到的位置都走了，可以出列了。

然后再从前往后，依次枚举 $V_{1}$ 中的点，寻找能到达的位置，记作 $V_{2}$ 放入队列，依次类推。

cpp

int dis[1001][1001];//初始都是inf
q.push((node){x,y});//初始位置放入队列
while(!q.empty())
{
    node now=q.front();//取队列的首部
    int x=now.x,y=now.y;
    q.pop();//删除队首
    for(枚举走一步能到达的位置(tx,ty))
    {
        if(dis[tx][ty]!=inf) continue;
        //如果这个位置已经被走到过了，那么不可能比dis[x][y]+1还远，因为之前枚举到的点的dis不大于dis[x][y]
        dis[tx][ty]=dis[x][y]+1;//更新到这个点的最短距离
        q.push((node){tx,ty});//把(tx,ty)放入队列。
    }
}

这样可以做到每个点得到的都是最短距离，因为我们相当于是先得到了所有走一步能到达的位置，然后再从所有走一步能到达的位置出发，到达所有走两步能到达的位置，以此类推。

根据这个算法，在任意时刻，队列里的点距离起点的距离之差不超过 $1$ 。

假设队列前一半距离是 $x$ ，中间一段距离是 $x + 1$ ，最后一段距离是 $x + 2$ ，那么我们现在要拿来扩展的点距离是 $x$ ，它扩展到的点距离应该是 $x + 1$ ，所以距离 $x + 2$ 的点此时不应该出现在队列里。

根据这个性质，也不会发生距离为 $x$ 的点到达某个距离比 $x$ 更小的点，所以已经到达过的点第二次再达到，答案不会更优。

P1443 马的遍历

P1135 奇怪的电梯

双向搜索

搜索树的节点个数并不是线性增长的，比如一个节点可以有两个子节点，那么规模为 $n$ 的数据，可能有 $2^{n}$ 个节点。

如果我们可以每次搜一半的数据，然后将两部分拼起来，那么就会变成 $2^{\frac{n}{2}} * 2$ 个节点。效果群拔！

比如上述问题，如果我们知道起点和终点，想问从起点走到终点至少需要多少步？

可以从起点和终点同时开始 $B F S$ ，如果某一个点被从两个方向遍历到了，那么将两个答案加起来就是最终答案了。

P1379 八数码难题

$3 * 3$ 的棋盘上有 $1 \sim 8$ 和一个空位，每次可以把一个数字和空位交换位置，最少多少次交换能变成给定的形态？

我们用 $v 1 []$ 和 $v 2 []$ 来标记某个状态是否到达过。可以从初始状态和目标状态同时开始 $B F S$ ，将初始状态的标识符设为 $1$ ，目标状态的标识符设为 $2$ ，每当初始状态拓展到一个新位置，把 $v 1$ 标记，目标状态拓展到新位置就把 $v 2$ 标记，如果一个位置的 $v 1, v 2$ 都被标记了，就说明会和了，把从两个方向来的步数加起来就可以了。