KMP
字符串匹配
给两个字符串
例如:
s = ababacabaca
t = abaca2
则一共出现了两次,分别是
暴力法字符串匹配,一般是
string s,t;
cin>>s>>t;
int sum=0;
int n=s.length(),m=t.length();
s=" "+s,t=" "+t;
for(int i=1;i<=n-m;++i)
{
bool flag=1;
for(int j=1;j<=m;++j)
{
if(s[i+j]!=t[j])
{
flag=0;break;
}
}
if(flag) ++sum;
}2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
来实现一下模拟过程:
当
ababacabaca ababacabaca ababacabaca
abaca abaca abaca
↑ ↑ ↑2
3
我们匹配上了三个,然后后面失配了。
当
ababacabaca
abaca
↑2
3
一个都没匹配上
当
ababacabaca
abaca
↑2
3
这里匹配的时候,注意到一个信息,在之前的匹配中,我们知道
而且我们还知道
这样可以还不够明显,我们换一个例子:
s=abcxabcxabcy
t=abcxabcy2
开始匹配:
abcxabcxabcy abcxabcxabcy abcxabcxabcy
abcxabcy abcxabcy abcxabcy
↑ ↑ …… ↑2
3
匹配到上述位置
满足
abcxabcyabc abcxabcyabc abcxabcyabc
abcyabc abcyabc abcyabc
↑ ↑ ↑2
3
这三次都是直接失败
abcxabcxabcy
abcyabc2
当匹配到这里的时候,我们知道刚才在第一次的时候满足
而且
那么说明
也就是说,这次匹配接着去比较
总结一下:
如果当前
那么,当以
这里
abcxabcxabcy abcxabcxabcy
abcxabcy abcxabcy
↑↑↑ ↑↑↑ ↑↑↑2
3
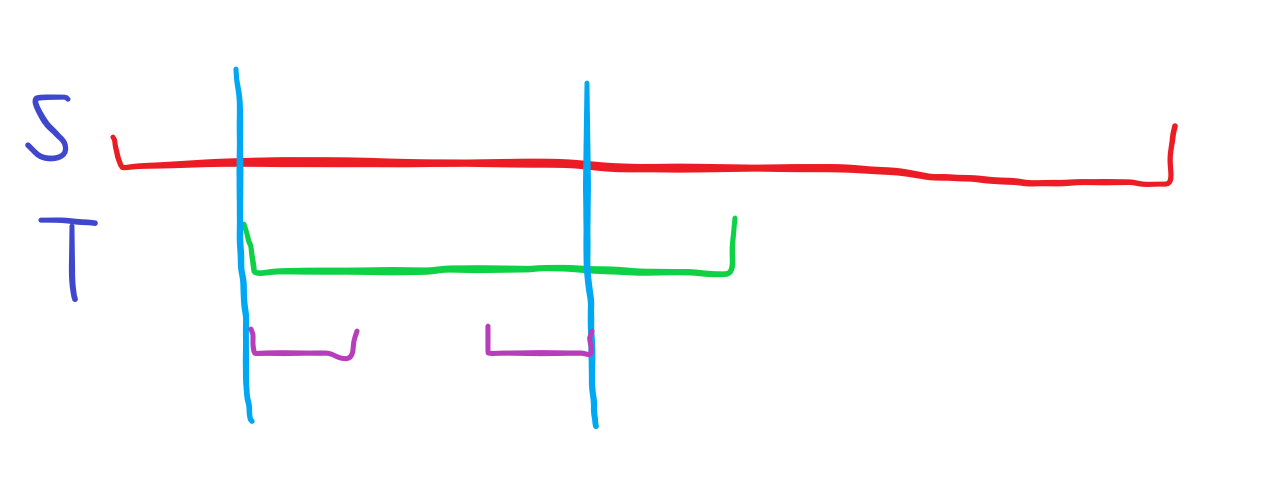
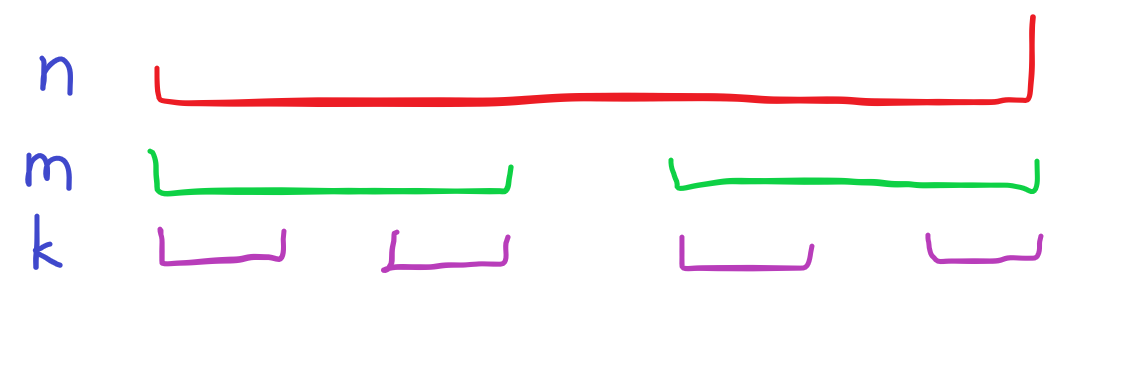
上图中,红色串是
同时可以证明,这中间的位置
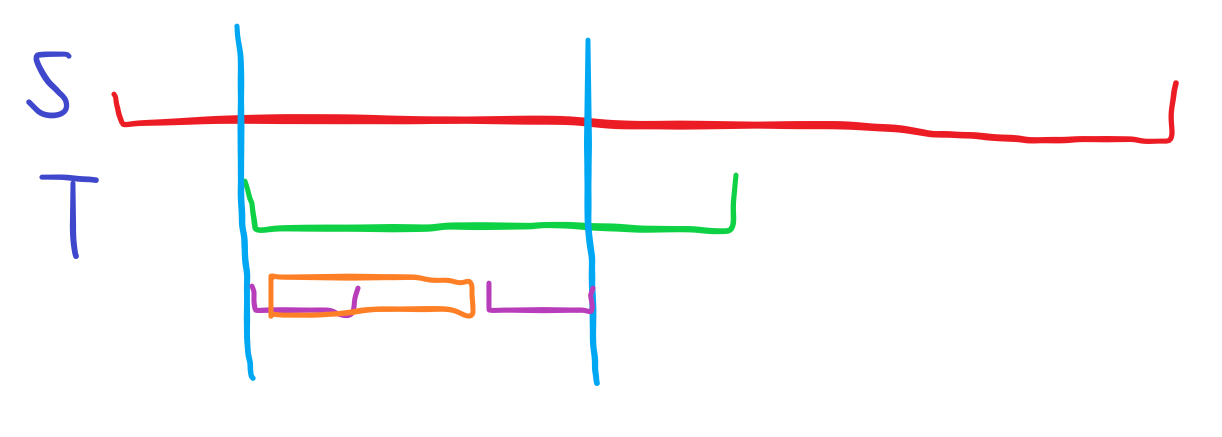
如果存在
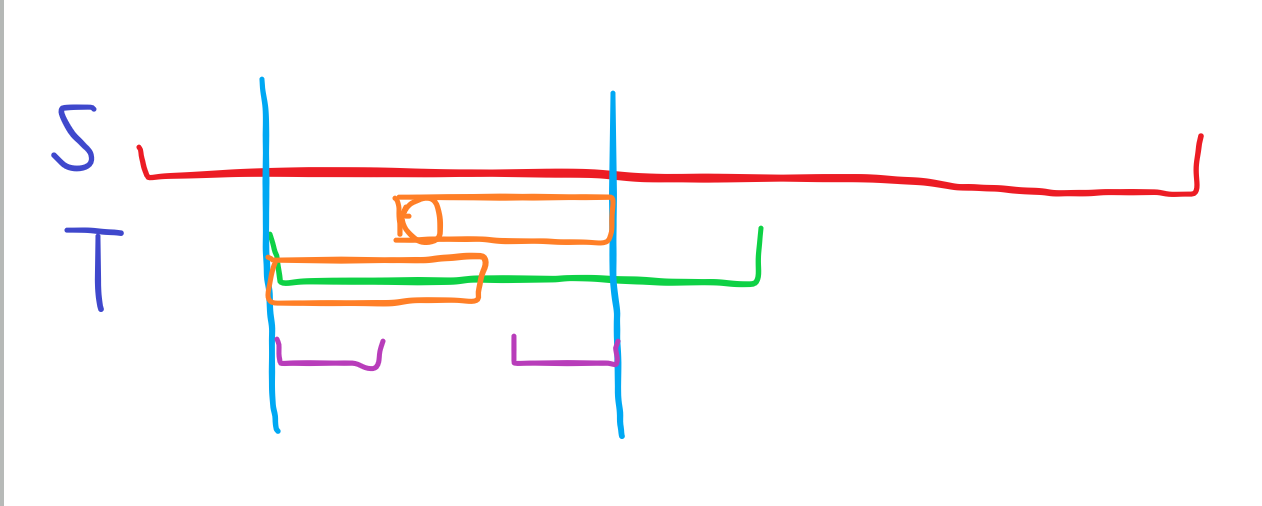
橙色部分原本是匹配
如果能匹配上,那么橙色部分必然是一个
所以橙色圆圈位置是不可能作为起点的。
那么当匹配失败后,可以直接跳到最长
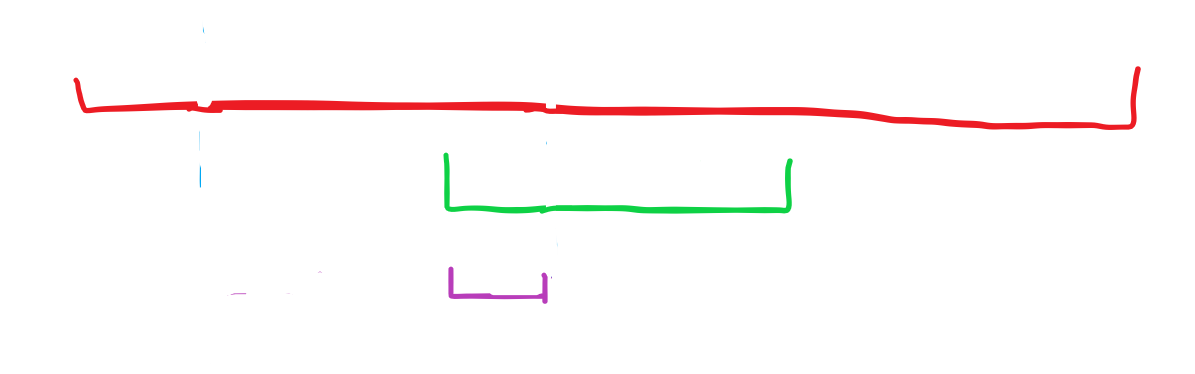
即:
abcxabcxabcy abcxabcxabcy
abcxabcy abcxabcy
↑↑↑ ↑↑↑ ↑↑↑2
3
综上:每次匹配失败后,跳转到当前匹配到的前缀的
那么问题的关键就是,怎么求出
有一个性质,
比如
然后
那么长度
如图,
由此得出一个基于递推的求前缀
设
一开始令
如果
如果匹配失败,那么说明从
但是
这部分的时间复杂度分析:每次向后匹配一位的时间复杂度是
因为每次跳
注意是跳
string s,t;
cin>>s>>t;
int n=s.length(),m=t.length();
s=" "+s;
t=" "+t;
vector<int> nxt(m+1);
int j=0;
for(int i=2;i<=m;++i)
{
while(j>0&&t[i]!=t[j+1]) j=nxt[j];
if(t[i]==t[j+1]) nxt[i]=++j;
}2
3
4
5
6
7
8
9
10
11
12
求出
j=1;
for(int i=1;i<=n;++i)
{
while(j>1&&s[i]!=t[j]) j=nxt[j-1]+1;
if(s[i]==t[j])
{
if(j==m)
{
cout<<i-m+1<<'\n';
j=nxt[j]+1;
}
else ++j;
}
}2
3
4
5
6
7
8
9
10
11
12
13
14
循环节
给定一个字符串
也就是整个字符串可以分成以下部分:
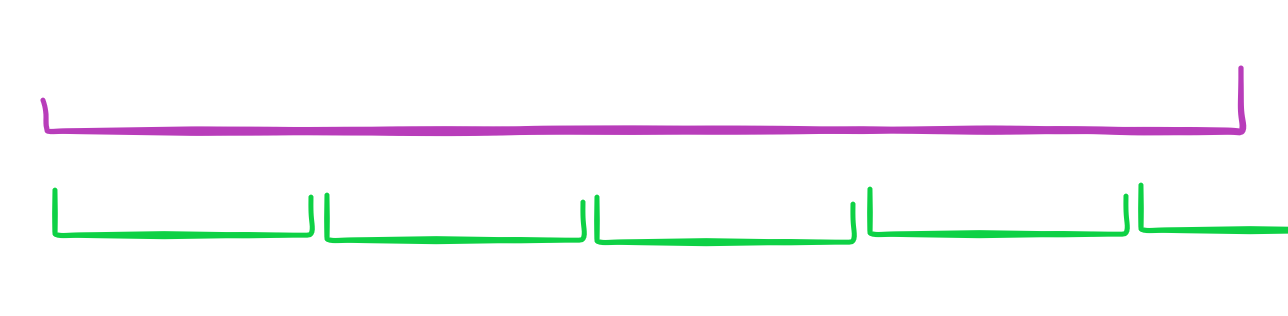
那么绿色部分就是紫色串
我们把第一个绿色部分删去,得到蓝色部分:
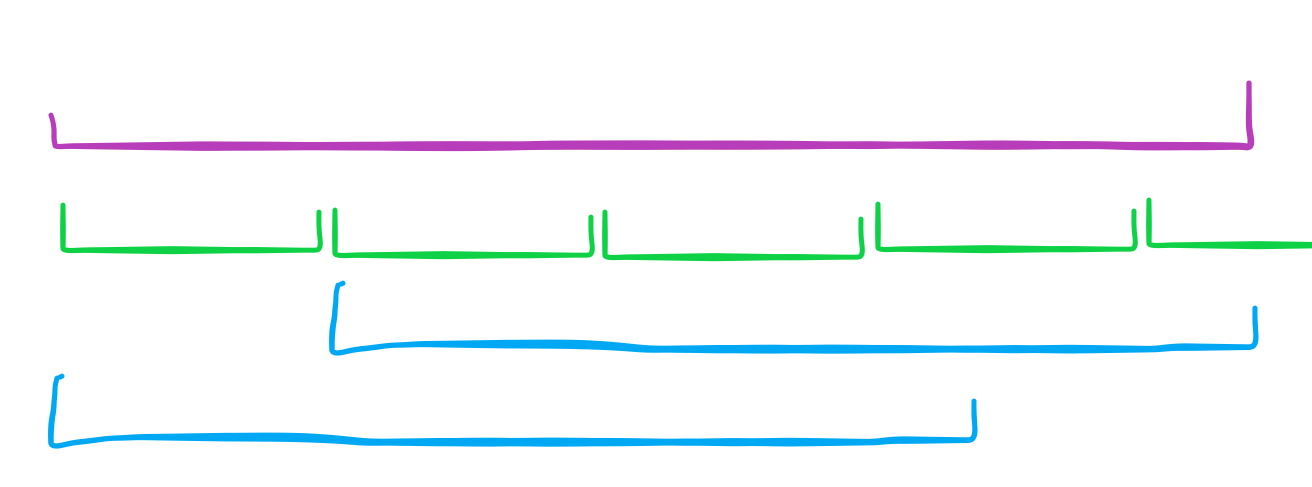
而因为绿色是循环的,所以两段蓝色部分恰好形成一个
反过来考虑,最短循环节就是整个字符串的长度减去最长
练习题
P4391 [BOI2009] Radio Transmission 无线传输
P1470 [USACO2.3] 最长前缀 Longest Prefix
